Contracts and Assertions

Flex supports SMT-based verification, which is a verification technique distinct from testing. The advantage of SMT-based verification is that false-positive results are impossible (or at least extremely unlikely). In practice, just because code performs well under black-box testing (e.g., unit testing or fuzz testing) does not guarantee that the code is safe. This is because it is infeasible to test the code for all possible inputs. SMT-based verification digs into the logic of the code to exhaustively consider every possible input in its analysis.

Type of Result	SMT-based Verification	Black-box Testing
False Positive	impossible	possible
False Negative	impossible	impossible
Unknown	possible	impossible

Basic Flex Contracts

Here's an example of a basic Flex contract:

contract average_example_1 {
    let x: int32 = 10;
    let y: int32 = 20;
    let average: int32 = (x + y) / 2;
    assert (x <= average && average <= y)
        || (y <= average && average <= x);
}

Contracts begin with the contract keyword followed by a name and contain Flex code in its curly braces. Any code you could expect writing in a Flex function will be valid within a contract. A typical use would involve using the assert keyword to describe desirable properties about your code. This should be familiar to those who have written unit tests before. However, contracts will check more than just assertions.

You can think of a Flex contract as a statement that claims "this code doesn't fail." There are several ways Flex code can fail:

• An assert statement evaluates to false.
• A division by zero occurs.
• The discriminee of a match expression does not have a pattern that matches it.
• A struct or newtype is constructed that violates a field constraint.
• An array is indexed at a position out of bounds.

The contract average_example_1 checks that the average of the numbers 10 and 20 sits between 10 and 20. There are two possible points of failure: the division in the computation of average and the assert statement that follows.

The Flex Contracts Panel

Flex contracts can be verified in Tangram Pro:

1. Go to FlexLang and open the Package Manager
2. Open a Flex file, add contracts, and save
3. Select the Flex Contracts tab at the bottom of the file
4. Click the Check all Flex Contracts button

Here's the results of checking the average_example_1 contract from above. The contract passes because neither of the two points of failure can be triggered.

Contracts with Parameters

Contracts can take parameters. The meaning of contracts that take parameters is "this code doesn't fail for any values of the parameters." Let's generalize average_example_1 from above to check that the average of any two numbers must sit between them.

contract average_example_2(x: int32, y: int32) {
    let average: int32 = (x + y) / 2;
    assert (x <= average && average <= y)
        || (y <= average && average <= x);
}

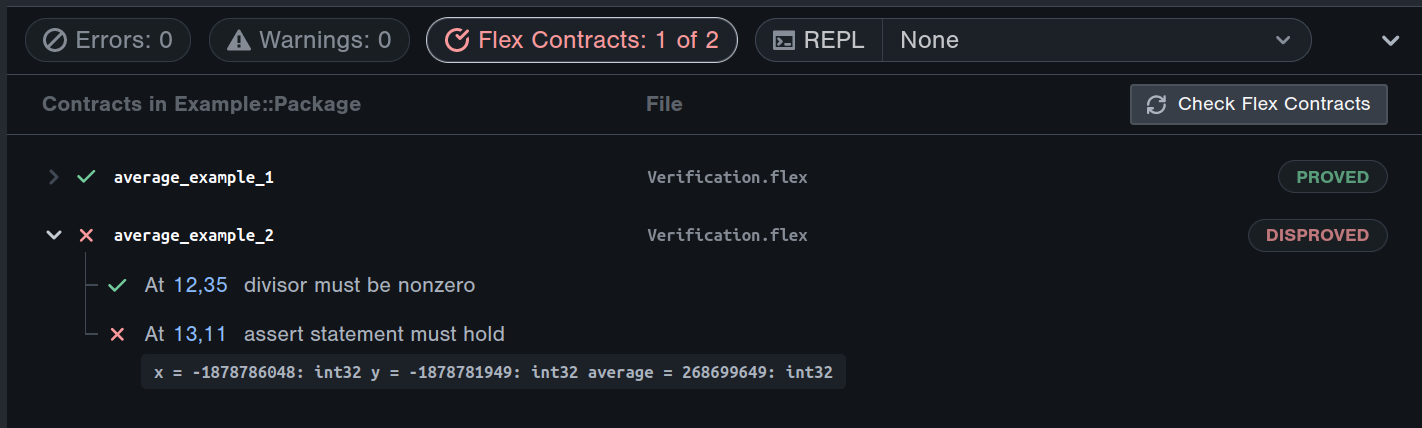
The SMT solver disproves this contract and informs us that when x = -1878786048 and y = -1878781949, the assert statement on line 13 does not hold. It turns out that these two numbers are so negative that their addition overflows the bounds of a 32-bit signed integer and wraps around to a positive number. A positive number certainly does not sit between two negative numbers.

Let's fix the contract to avoid any addition that can overflow:

contract average_example_3(x: int32, y: int32) {
    let average: int32 = x - x/2 + y/2;
    assert (x <= average && average <= y)
        || (y <= average && average <= x);
}

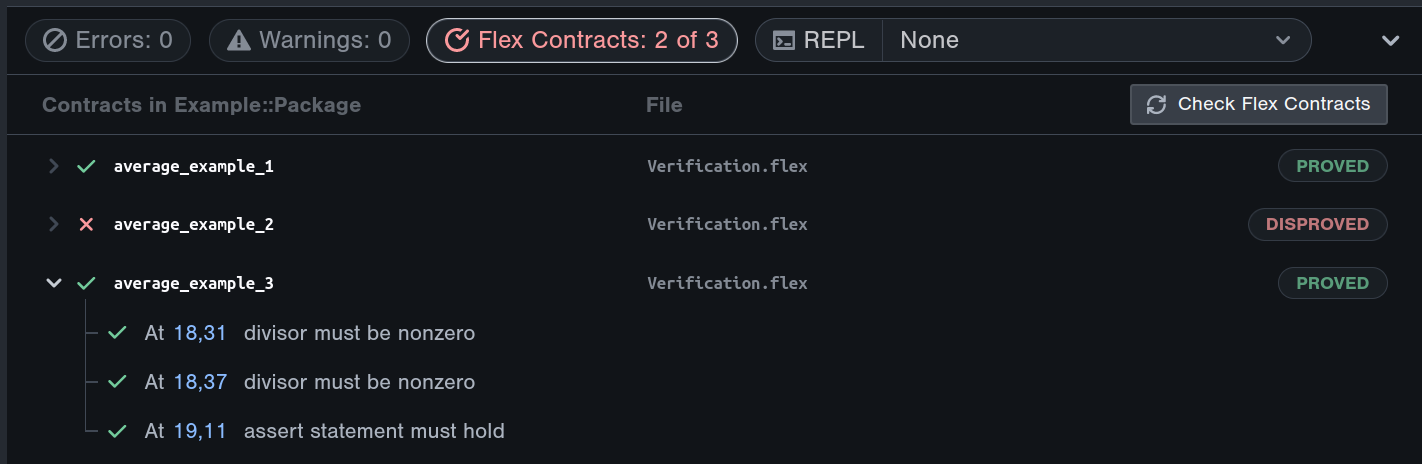
We can see the power of SMT-based verification at work! In a fraction of a second, we verified that this formula x - x/2 + y/2 for computing an average is safe for any pair of numbers x and y. To get that same level of certainty with black-box testing, we would need to manually test the property for all inputs. If testing a single input takes one nanosecond, then testing all 2⁶⁴ possibilities would take over 500 years!

How can correctness be proved?

Think back to math class. How would you solve equations like x^2 - x = 6? Would you plug in every possible number for x until you found one that works? Of course not! You manipulate the equation to solve for values of x that satisfy the equation (in this case 3 or -2).

Under the hood, an SMT solver is doing something very similar to what you did in math class. It is attempting to find solutions by manipulating the code as a mathematical expression. In particular, it is solving for parameter values that cause the code to fail. For many programs, "solving for failure" is orders of magnitude faster than attempting to find failures by brute-force.

Think again back to math class, and this time you need to find real-number solutions to the equation x^2 + x + 1 = 0. You may think to use the quadratic formula. The quadratic formula gives you two complex solutions (1+2i, 1-2i) and no real solutions. Real solutions, if they exist, must come from the quadratic formula, so you have proven that there aren't any. It's not that you've tried a bunch of real numbers and none of them worked. There are none to find in the first place!

Once again the SMT solver is doing something very similar. In the process of "solving for failures," it may discover that there can be no failures. Thus, the correctness of the code is proved.